Contenuto

• passi
• Suggerimenti

I matematici e i programmatori grafici hanno spesso bisogno di trovare l'angolo tra due vettori. Fortunatamente, la formula utilizzata per calcolare questo angolo non richiede altro che un semplice prodotto scalare. Sebbene il ragionamento alla base di questa formula sia più facile da capire quando si utilizzano vettori bidimensionali, possiamo facilmente adattarlo a vettori con qualsiasi numero di componenti.

passi

Parte 1 di 2: calcola l'angolo tra due vettori

1. 

   Identifica i due vettori. Annotare tutte le informazioni note sui due vettori. Ai fini di questo tutorial, assumeremo che tu conosca i vettori solo in termini di coordinate dimensionali (chiamate anche componenti). Se conosci già il file modulo o standard di questi vettori (ovvero la loro lunghezza), puoi saltare alcuni dei passaggi seguenti.
   • Esempio: considereremo i vettori bidimensionali = (2,2) e = (0,3). Questi due vettori possono essere riscritti come = 2io + 2j e = 0io + 3j = 3j.
   • Sebbene il nostro esempio utilizzi due vettori bidimensionali, possiamo applicare le seguenti istruzioni a vettori con qualsiasi numero di componenti.

2. 

   
   
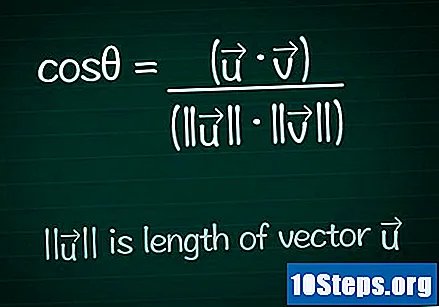
   Scrivi la formula del coseno. Per trovare il valore dell'angolo θ tra due vettori qualsiasi, dobbiamo prima calcolare il coseno di quell'angolo. Puoi cercare e scoprire la formula in dettaglio o semplicemente scriverla così com'è di seguito:
   • cosθ = (•) / (|||| ||||)
   • |||| rappresenta il modulo (o lunghezza) del vettore ".
   • • rappresenta il prodotto scalare (o prodotto interno) dei due vettori.

3. 

   
   
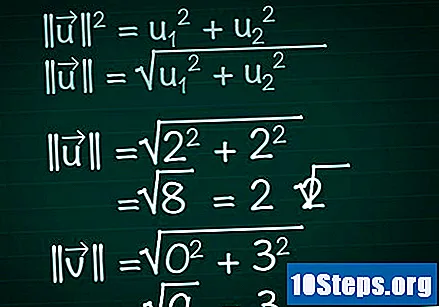
   Calcola il modulo di ogni vettore. Immagina un triangolo rettangolo formato dal componente X di un vettore, la sua componente y e il vettore stesso. In questo triangolo, il vettore gioca il ruolo dell'ipotenusa; quindi, per trovarne la lunghezza, applicheremo il teorema di Pitagora. Di conseguenza, questa formula è facilmente applicabile a vettori con un numero qualsiasi di componenti.
   • || u || = u₁ + u₂. Se il vettore ha più di due componenti, continua ad aggiungere + u₃ + u₄ +...
   • Pertanto, per un vettore bidimensionale, dovremo || u || = √ (u₁ + u₂).
   • Nel nostro esempio, |||| = √ (2 + 2) = √ (8) = 2√2. |||| = √(0 + 3) = √(9) = 3.

4. 

   
   
   Calcola il prodotto scalare tra i due vettori. Dovresti già conoscere il metodo per moltiplicare i vettori, chiamato anche prodotto scalare. Per calcolare il prodotto scalare di due vettori in termini di componenti, moltiplichiamo i componenti nella stessa direzione tra loro e quindi aggiungiamo i risultati di quei prodotti.
   • Se lavori con programmi di grafica per computer, visita prima la sezione "Suggerimenti" prima di procedere.
   • In termini matematici, • = u₁v₁ + u₂v₂, dove u = (u₁, u₂). Se il tuo vettore ha più di due componenti, continua ad aggiungere + u₃v₃ + u₄v₄...
   • Nel nostro esempio, • = u₁v₁ + u₂v₂ = (2)(0) + (2)(3) = 0 + 6 = 6. Questo è il valore del prodotto scalare tra i vettori e.

5. 

   Sostituisci questi risultati nella formula del coseno. Ricorda, cosθ = (•) / (|||| || ||). Abbiamo già calcolato il prodotto scalare e il modulo dei due vettori. Ora, sostituiamo questi valori nella formula e calcoliamo il coseno dell'angolo.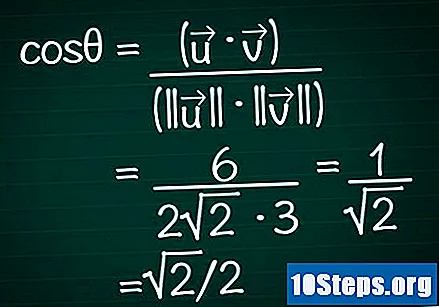
   • Nel nostro esempio, cosθ = 6 / (2√2 * 3) = 1 / √2 = √2 / 2.

6. 

   Trova l'angolo in base al tuo coseno.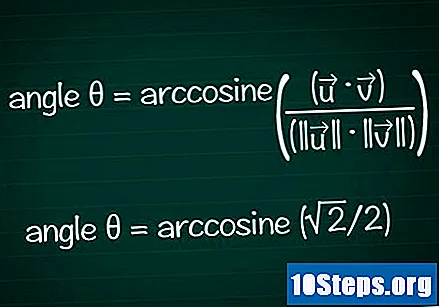
   Usa la funzione arco o cos della calcolatrice per determinare l'angolo θ dal valore del coseno. In alcuni casi, potresti essere in grado di trovare il valore dell'angolo in base al cerchio unitario.
   • Nel nostro esempio, cosθ = √2 / 2. Digita "arccos (√2 ​​/ 2)" nella calcolatrice per trovare l'angolo. Un'altra opzione è cercare l'angolo θ del cerchio unitario dove cosθ = √2 / 2: questo sarà vero per θ = /₄ o 45 °.
   • Mettendo insieme tutte le informazioni, avremo la formula finale θ = arccosine ((•) / (|||| || ||))

Parte 2 di 2: definizione della formula per il calcolo dell'angolo

1. 

   Comprendi lo scopo della formula. La formula che abbiamo usato per calcolare l'angolo tra due vettori non era derivata da regole preesistenti; invece, è stato creato come una definizione del prodotto scalare tra due vettori e l'angolo tra di loro. Tuttavia, questa decisione non è arbitraria. Con uno sguardo più da vicino alla geometria di base, possiamo capire perché questa formula si traduce in definizioni così utili e intuitive.
   • I seguenti esempi fanno uso di vettori bidimensionali perché sono il tipo più intuitivo con cui lavorare. I vettori di tre o più dimensioni hanno le loro proprietà definite dalla formula generale (anche in modo molto simile).

2. 

   Rivedi la legge del coseno. In ogni triangolo, considera l'angolo θ formato dai lati Il e B e il lato ç opposto a quell'angolo. Secondo la legge del coseno, c = a + b -2abcintura(Θ). La dimostrazione di questa formula può essere facilmente ottenuta dalla conoscenza della geometria di base.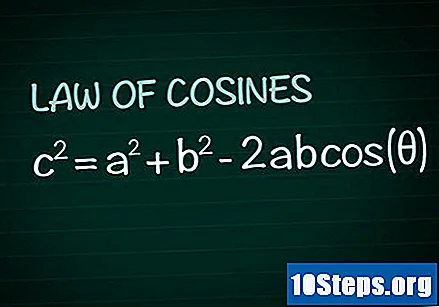

3. 

   Collega i due vettori per formare un triangolo. Disegna una coppia di vettori e, con un angolo θ tra di loro. Quindi, disegna un terzo vettore tra di loro per formare un triangolo. In altre parole, disegna il vettore in modo tale che + = o semplicemente = -.

4. 

   Applica la legge del coseno a questo triangolo. Sostituisci la lunghezza dei lati del nostro triangolo vettoriale (cioè il modulo vettoriale) nella formula per la legge del coseno:
   • || (a - b) || = || a || + || b || - 2 || a || || b ||cintura(θ)

5. 

   Riscrivi la formula usando prodotti scalari. Ricorda che il prodotto scalare è l'ingrandimento di un vettore proiettato su un altro. Il prodotto scalare di un vettore stesso non richiede proiezione perché non vi è alcun cambiamento di direzione. Ciò significa che • = || a ||. Sulla base di queste informazioni, riscriviamo l'equazione della legge del coseno:
   • (-) • (-) = • + • - 2 || a || || b ||cintura(θ)

6. 

   Semplifica la formula. Espandi i prodotti sul lato sinistro dell'equazione e poi semplifica fino a raggiungere la formula che conosciamo per il calcolo degli angoli.
   • • - • - • + • = • + • - 2 || a || || b ||cintura(θ)
   • - • - • = -2 || a || || b ||cintura(θ)
   • -2 (•) = -2 || a || || b ||cintura(θ)
   • • = || a || || b ||cintura(θ)

Suggerimenti

• Per una rapida risoluzione, applica la seguente formula a qualsiasi coppia di vettori bidimensionali: cosθ = (u₁ • v₁ + u₂ • v₂) / (√ (u₁ • u₂) • √ (v₁ • v₂)).
• Se lavori con programmi di computer grafica, molto probabilmente avrai bisogno di conoscere solo la direzione dei vettori, non la loro lunghezza. Segui i passaggi seguenti per semplificare le equazioni e velocizzare il tuo programma:
  • Normalizza ogni vettore, ovvero trova il vettore unitario che ha la stessa direzione del vettore originale. Per fare ciò, dividi ogni componente del vettore per il modulo del vettore.
  • Calcola il prodotto scalare dei vettori normalizzati, non i vettori originali.
  • Poiché il modulo (cioè la lunghezza) dei vettori normalizzati è unitario, possiamo escluderli dalla formula. La tua equazione finale per il calcolo degli angoli sarà gli archi (•).
• Sulla base della formula della legge del coseno, possiamo scoprire rapidamente se l'angolo in questione è acuto o ottuso. Inizia con cosθ = (•) / (|||| ||||):
  • I lati sinistro e destro dell'equazione devono avere lo stesso segno (positivo o negativo).
  • Poiché le lunghezze sono sempre positive, cosθ avrà sempre lo stesso segno del prodotto scalare.
  • Pertanto, se il prodotto scalare è positivo, cosθ sarà positivo. Ciò significa che l'angolo si trova nel primo quadrante del cerchio unitario, ovvero θ <π / 2 o 90 °. Pertanto, l'angolo è acuto.
  • Se il prodotto scalare è negativo, cosθ è negativo. Ciò significa che l'angolo si trova nel secondo quadrante del cerchio unitario, ovvero π / 2 <θ ≤ π o 90 ° <θ ≤ 180 °. Pertanto, l'angolo è ottuso.